最近的随机过程作业涉及到了value iteration和policy iteration，于是就去搜了相关的网课CS229-lecture17来看，讲的很好，于是做了一些笔记。
由于这些东西和强化学习能扯上一点关系，所以就分类到了强化学习。

关于π和$V^{\pi}$

π是optimal polocy，是一个state -> action 的映射

比如：

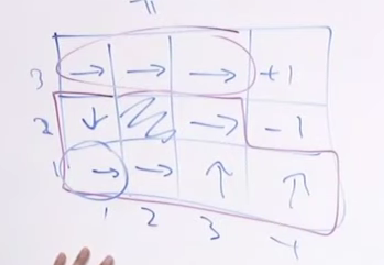
$V^{\pi}$ 是 从某一个位置开始(当作初始位置) 所获得的一个 reward

bellman equation

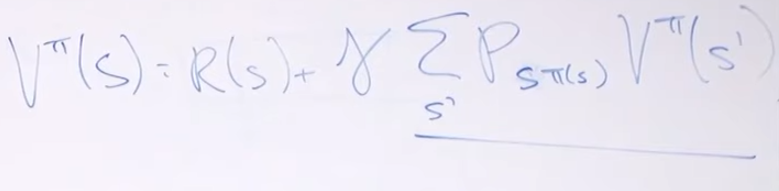
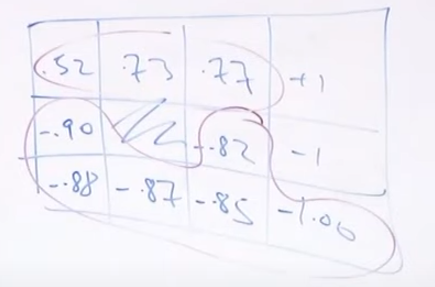
例子

比如说要求 (3,1) 这个位置的 $V^{\pi}$

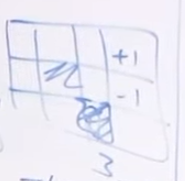
那么求法就是：

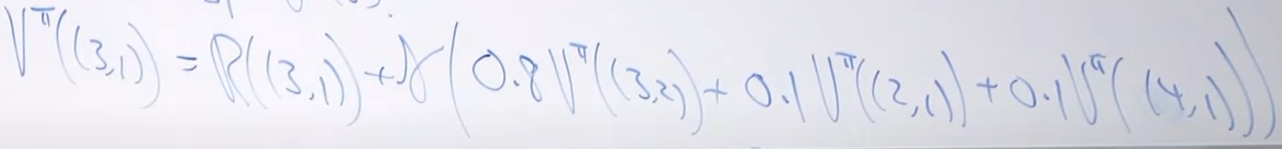
如果把每一个状态对应的$V^{\pi}$当作是一个未知数，由于已经给出了确定的policy $\pi$ (也就是说action是确定的)，那么根据bellman equation，每一个$V^{\pi}$都可以写出一个方程。所以可以用一个linear solver来构建方程并且求解。

关于$\pi^*$ 和 $V^*$

$\pi^*$ 是 optimal policy

$V^*$是 optimal policy 对应的value function，公式如下：

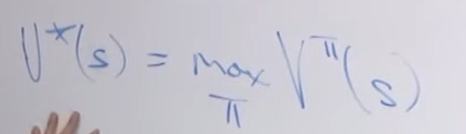
对应的bellman equation

value iteration

由于V(s)直接存在相互依赖关系，value iteration有两种，一种是 synchrounous，就是每一个V(s)同步更新，另一种就是asynchrounous，就是V(s)的更新不同步。不过都差不多。

经过多次迭代，V就会很快收敛到V*。最后收敛完毕后，再去计算对应的 π(s) 。

policy iteration

policy iteration的重点在于π，在循环中。

第一步：根据 π(s) 计算出对应的V。 如何计算? -> 如前面所述，使用linear solver来计算。

第二步：假设V是optimal value function，即V*，然后更新 π(s)。

pros and cons of two methods

由于policy iteration实际是一个 linear solver based 的 方法，所以当状态数很少时，求解速度很快，但是当状态数目很多时，求解速度就会变慢。所以在状态数目很多时，倾向于使用 value iteration。