Assignment1

运行结果

关于三角形颠倒的解决方法，请见 结果出现上下颠倒，怎么办？只加一个负号即可 – 计算机图形学与混合现实研讨会 (games-cn.org)

实现细节

详细代码请见：详细代码

实现了main.cpp中的get_model_matrix, get_rotation, get_projection_matrix函数。

其中每一个的实现基本都能在下面的相关知识找到对应，无非就是把矩阵用代码写出来了而已。

这里记录一个需要注意的点，就是在get_projection_matrix函数中，在设置n和f(近平面和远平面)时，需要加一个负号：

float n = -zNear;
float f = -zFar;

相关知识

关于三维的变换

一般的旋转变换

旋转变换（一）旋转矩阵Frank的专栏-CSDN博客旋转变换矩阵

绕任意轴的旋转变换

MVP

M: Model transformation

模型变化，应该就是指模型的变化。包括平移、旋转、放缩等等操作。

在本次的作业中指的就是绕z轴旋转，这对应一个变换矩阵。

V: View transformation

视图变换，指的就是从相机出发观测物体，那么就需要将相机移动到原点，并且面朝-z方向，向上方向为y轴正方向。

将相机移动后，我们需要也对物体做一个移动，来保持相对位置不变。所以最后的结果就是，我们直接假定相机在原点，面朝-z方向，向上方向为y轴正方向，然后只对物体做这个变换就行了。

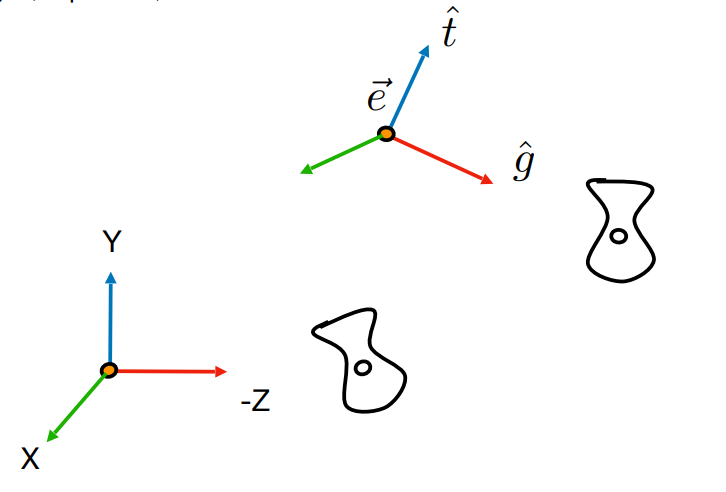
该变换分为两步：

这里我们把视图变换的矩阵令为 $M_{view}$ ,平移矩阵令为 $T_{view}$ ,旋转矩阵令为 $R_{view}$

1. 将相机移动到原点

   平移矩阵为 $T_{view}$

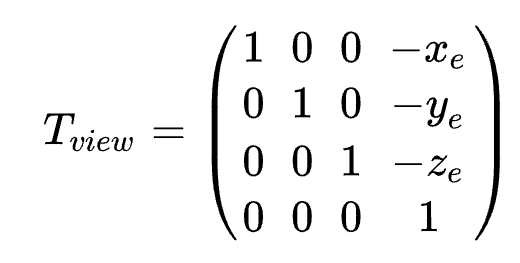
1. 将相机旋转到面朝-z方向，且上方为y正方向。

   直接对$R_{view}$ 进行求解比较困难，所以我们转而去求它的逆变换，即将处于原点，面向-z，上朝y的相机旋转到当前的相机位置，用$R_{view}^{-1}$表示，那么有：

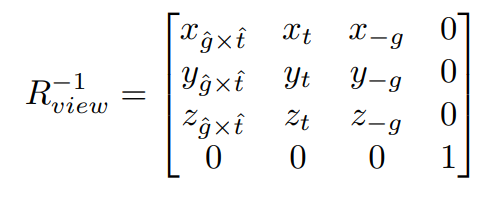
​ 因为旋转矩阵是一个正交矩阵，所以矩阵的逆等于矩阵的转置，因此我们可以求得$R_{view}$：

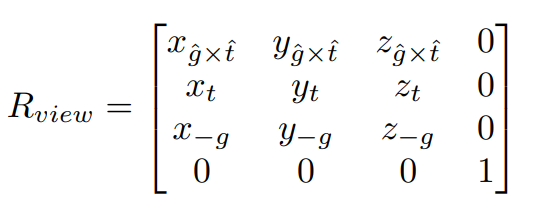
因为模型变换和视图变化都是在物体上进行变化，所以一般我们把他们一起叫做模型视图变换。

P：Perspective projection

正交投影(Orthographic projection)

正交投影就是在空间中确定一个立方体 (用来表示相机的可视区域)，对应六个面在不同坐标轴下的距离为right, left, top, bottom, near, far，要做的事情就是把这个立方体移动到原点，并且缩放到 (-1, 1)。

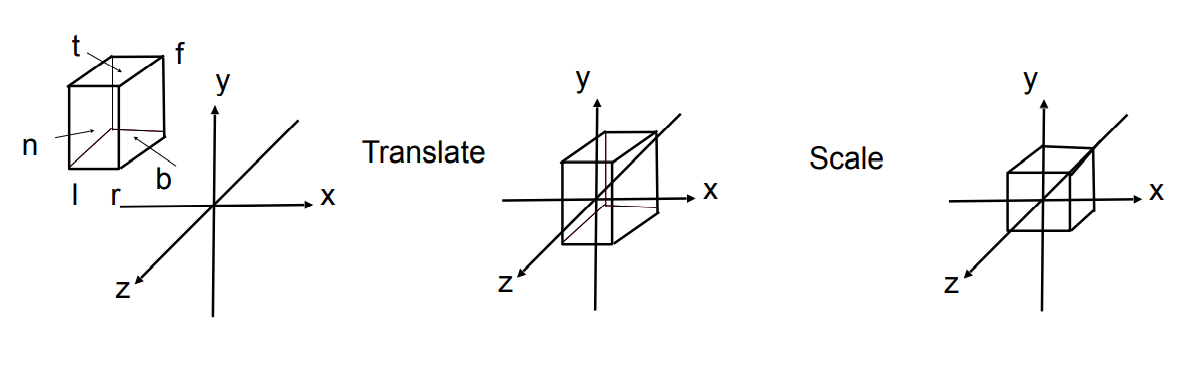
对应的矩阵$M_{ortho}$ 为：

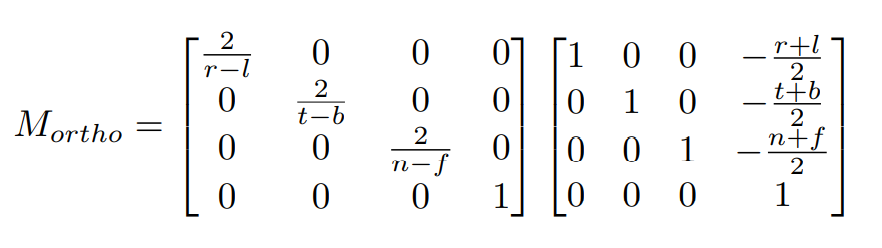
透视投影(Perspective projection)

矩阵推导

透视投影就是将正交投影里面的一个立方体变成了一个forstum，我们要做的就是先将这个forstum "挤" 成一个立方体，然后后续操作就和正交投影一样了。

其中，透视投影变换矩阵为 $M_{persp}$ ，我们只需要去求透视投影向正交投影的变换矩阵 $M_{persp->ortho}$ 即可

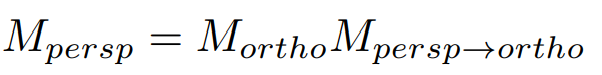
$M_{persp->ortho}$ 的求法比较发杂，下面贴一些图：

• 对于当$M_{persp->ortho}$ 作用到(x,y,z,1)后，对于frostum里的每一个点，可以得到：

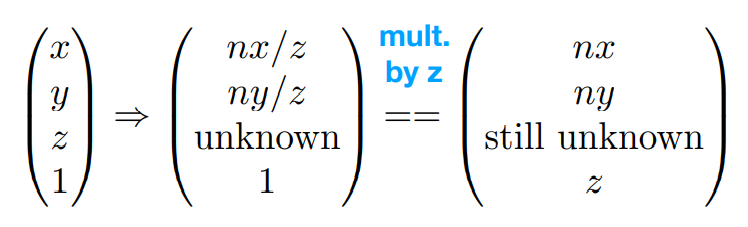
• 根据这个，我们已经可以得出矩阵中的大部分元素

• 再根据下面标红的两个发现(近平面的点不会变，远平面的z不会变)列出公式，求解最后剩余的？

于是就求解得到$M_{persp->ortho}$ 了。

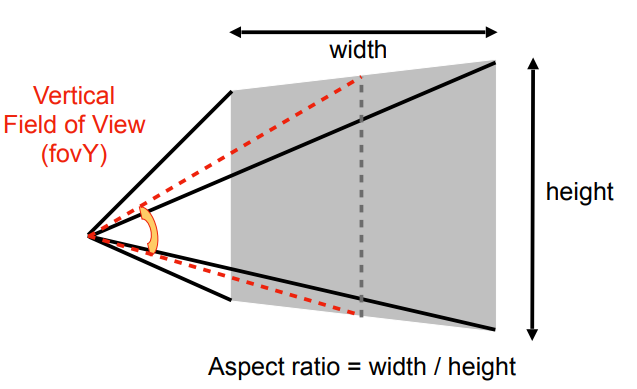
fov与aspect ratio

fov是(field of view)，即竖直方向的可视角度

aspect ratio是width/height

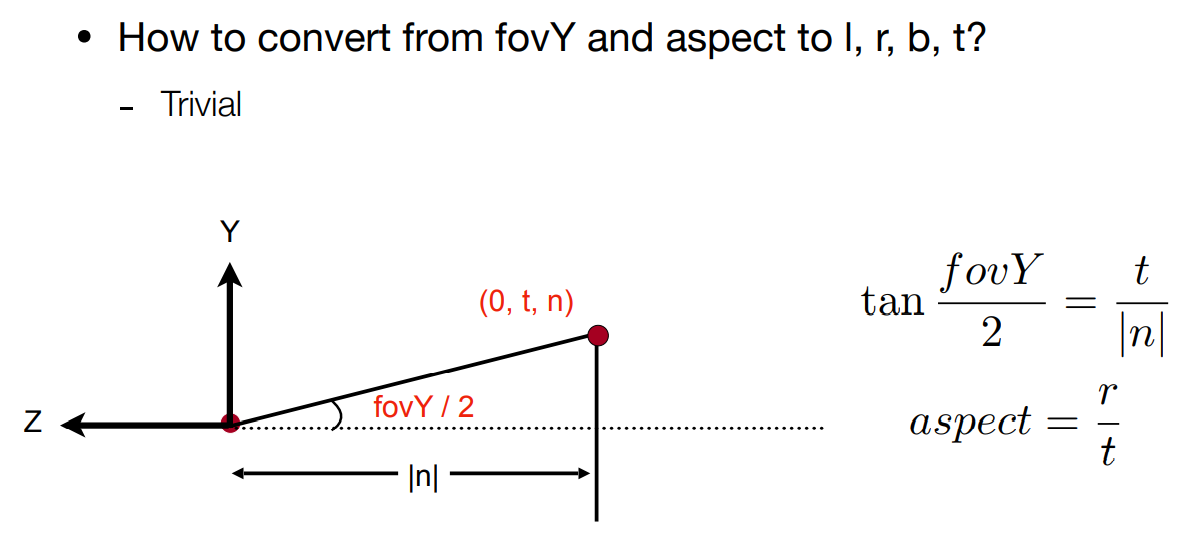
只需要使用fov和aspect ratio就可以用来表示一个透视投影(n和f是给定的，所以我们再把fov和aspect ratio转换为l, r, b, t即可)